A energia não pode ser criada nem destruída, mas sim transformada. A energia pode ser obtida de diversas formas, sendo as modalidades mais comuns as descritas abaixo:
A energia cinética é inerente a corpos em movimento e pode ser obtida pela equação:
É a energia associada com a posição de um corpo em relação a um campo gravitacional.
É a energia armazenada por um sistema elástico ao ser tracionado ou comprimido, é expresso pela equação seguinte:
O trabalho de uma força é dado pelo produto escalar dos vetores força e deslocamento, dado por:
Onde o trabalho é uma grandeza escalar dada em Joules (J). Pela observação da equação (04) percebe-se que quando a força aplicada é perpendicular ao deslocamento do corpo, tem-se que o trabalho da força é nulo.

Em certos casos, o vetor força varia com a distância percorrida pelo corpo, nesta situação é possível calcular o módulo do trabalho realizado pelo cálculo da área sob a curva do diagrama (F x s).

O trabalho resultante de n forças é dado pela soma algébrica dos trabalhos realizados por cada uma das forças atuantes sobre o corpo:
A potência é a razão entre trabalho realizado por uma força e o intervalo de tempo. Por isso, temos que quando realizamos um mesmo trabalho em um menor intervalo de tempo, desenvolvemos maior potência. A potência é uma grandeza escalar e a sua unidade no SI é Watts (W).
Uma outra maneira de representar a potência é obtida pela substituição da equação (04) na equação (05):
Essa maneira é utilizada para se obter a potência necessária para manter um corpo em movimento retilíneo e uniforme.
O rendimento é dado pela razão entre a potência útil e a potência total fornecida, como mostrado abaixo:
(PUC-MG) Não realiza trabalho:
(PUC-BA) A força de módulo 30N atua sobre um objeto formando um ângulo constante de 60º com a direção do deslocamento do objeto. Dados: sen 60º = √3/2, cos 60º = 1/2. Se d = 10m, o trabalho realizado pela força, em joules, é igual a:
(UFRN) Um bloco é arrastado sobre um plano horizontal, com o qual possui coeficiente de atrito m, sofrendo um deslocamento horizontal de módulo d. Sendo N a intensidade da força de reação normal da superfície sobre o bloco, o trabalho da força de atrito, nesse deslocamento, é:
(UFES) A força \(\overrightarrow{F}\) desloca o bloco da figura ao longo da reta AB. A componente de \(\overrightarrow{F}\) que executa trabalho é:

A componente de \(\overrightarrow{F}\) que executa trabalho é:
(PUC-RJ) Durante a aula de educação física, ao realizar um exercício, um aluno levanta verticalmente um peso com sua mão, mantendo, durante o movimento, a velocidade constante.
Pode-se afirmar que o trabalho realizado pelo aluno é:
(UERJ) Um veículo consumiu 63,0 L de gás natural para percorrer uma distância de 225 km. A queima de 28,0 L de gás natural libera 1,00 × 10⁶ J de energia.
A energia consumida, em joules, por quilômetro, foi igual a:
(UCSA) Uma partícula de massa constante tem o módulo de sua velocidade aumentado em 20%. O respectivo aumento de sua energia cinética será de:
(INSPER) José Mário é um homem que mantém sua condição física fazendo caminhadas em torno do condomínio em que reside. Em dias de chuva, ele compensa subindo a escadaria do prédio, a partir do térreo até o seu apartamento, no 10º andar. O desnível entre 2 andares consecutivos é de 3,0 m José Mário pesa 800 N. Se fosse possível converter toda a energia potencial acumulada nessa subida em energia elétrica para acender um circuito de 10 lâmpadas de LED, de 5 W cada, o circuito permaneceria aceso, ininterruptamente, por
(IFBA) Um aquecedor de imersão, ligado a uma fonte de tensão contínua de 1,00 · 10² V, aquece 1,00 kg de água, de 15° C a 85 °C, em 836 s. Calcule a resistência elétrica do aquecedor, supondo que 70% da potência elétrica dissipada no resistor seja aproveitada para o aquecimento da água. Considere o calor específico da água: c = 4,18 · 10³ \(\frac{J}{kg}\) · K.
(MACKENZIE) Uma criança de massa 30,0 kg encontra-se em repouso no topo (A) de um escorregador de altura 1,80 m, em relação ao seu ponto mais baixo (B). Adotando-se o módulo da aceleração da gravidade g = 10,0 m/s² e desprezando-se todos os atritos, a velocidade da criança no ponto mais baixo é
(ITA) Um pingo de chuva de massa 5,0 x 10\(^{-5}\) kg cai com velocidade constante de uma altitude de 120 m, sem que a sua massa varie, num local onde a aceleração da gravidade tem módulo igual a 10 m/s². Nestas condições, a intensidade de força de atrito F do ar sobre a gota e a energia mecânica E dissipada durante a queda são respectivamente:
(UFRGS) Um dispositivo de lançamento vertical de massas consiste em um tubo com uma mola sobre a qual são colocados objetos. Após a mola ser comprimida, o sistema massa-mola é liberado. Não há contato entre a massa e a parede do tubo, e a resistência do ar é desprezível.
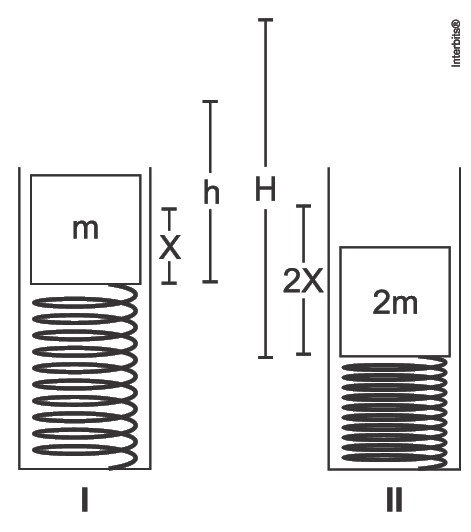
Na figura I, um objeto de massa m é colocado sobre uma mola de constante elástica k. A mola é então comprimida por uma distância X. Quando o sistema é liberado, o objeto é arremessado verticalmente e atinge uma altura h.
Na figura II, um objeto de massa 2 m é colocado sobre a mesma mola e esta é comprimida por uma distância 2 X. Nesse caso, a altura H atingida pelo objeto, após a liberação do sistema, é
(UNIFOR) Três esferas idênticas, de raios R e massas M, estão entre uma mesa horizontal. A aceleração local de gravidade tem módulo igual a g. As esferas são colocadas em um tubo vertical que também está sobre a mesa e que tem raio praticamente igual ao raio das esferas. Seja E a energia potencial gravitacional total das três esferas sobre a mesa e E’ a energia potencial gravitacional total das três esferas dentro do tubo. O módulo da diferença (E’ – E) é igual a:
(FUND. CARLOS CHAGAS) Uma mola elástica ideal, submetida a ação de uma força de intensidade F = 10 N, está deformada de 2,0 cm. A energia elástica armazenada na mola é de:
(FUVEST) Um ciclista desce uma ladeira, com forte vento contrário ao movimento. Pedalando vigorosamente, ele consegue manter a velocidade constante. Pode-se então afirmar que a sua:
(UEFS) Um carro de 1.000 kg com o motor desligado é empurrado em uma rua plana e horizontal por um grupo de pessoas que, juntas, exercem uma força constante e horizontal de 600 N sobre o veículo. A partir do repouso, o carro adquire uma velocidade de 2 m/s após percorrer 10 m em linha reta.

A energia dissipada ao final desses 10 m foi de
(UFSCAR-SP) O trabalho realizado por uma força conservativa independe da trajetória, o que não acontece com as forças dissipativas, cujo trabalho realizado depende da trajetória. São bons exemplos de forças conservativas e dissipativas, respectivamente:
(ITA-SP) A partir do repouso, um carrinho de montanha russa desliza de uma altura H = 20 √3 m sobre uma rampa de 60o de inclinação e corre 20 m num trecho horizontal antes de chegar em um loop circular, de pista sem atrito.

Sabendo que o coeficiente de atrito da rampa e do plano horizontal é 0,5, assinale o valor do raio máximo que pode ter esse loop para que o carrinho faça todo o percurso sem perder contato com a pista.
(FUVEST-SP) Um skatista treina em uma pista cujo perfil está representado na figura abaixo. O trecho horizontal AB está a uma altura h = 2,4 m em relação ao trecho, também horizontal, CD. O skatista percorre a pista no sentido de A para D.

No trecho AB, ele está com velocidade constante, de módulo v = 4 m/s; em seguida, desce a rampa BC, percorre o trecho CD, o mais baixo da pista, e sobe a outra rampa até atingir uma altura máxima H, em relação a CD. A velocidade do skatista no trecho CD e a altura máxima H são, respectivamente, iguais a
(PUC-RJ) Um ciclista tentando bater um recorde de velocidade em uma bicicleta desce, a partir do repouso, a distância de 1440 m em uma montanha cuja inclinação é de 30°. Calcule a velocidade atingida pelo ciclista ao chegar à base da montanha.
Dados: Não há atrito e g = 10 m/s²
(COLÉGIO NAVAL) Analise a figura
Dados: g = 10 m/s² e Mtrenó = 800 kg.

Numa determinada montanha russa um trenó, sob a ação de uma força resultante constante, que atua de A até B, parte do repouso do ponto A e, após 2 segundos, atinge a velocidade de 180 km/h no ponto B, iniciando uma subida que o leva até o ponto C, onde passa com velocidade de 18 km/h. Sabendo que a energia perdida pelos atritos entre os pontos B e C foi de 19.10⁴ J, é correto afirmar que a força resultante que atuou sobre o trenó entre os pontos A e B e a altura atingida por ele no ponto C são, respectivamente:
(FUVEST) Um pai de 70 kg e seu filho de 50 kg pedalam lado a lado, em bicicletas idênticas, mantendo sempre velocidade uniforme. Se ambos sobem uma rampa e atingem um patamar plano, podemos afirmar que, na subida da rampa até atingir o patamar, o filho, em relação ao pai:
(FUVEST) Uma empilhadeira elétrica transporta do chão até uma prateleira, a uma altura de 6,0 m do chão, um pacote de 120 kg. O gráfico ilustra a altura do pacote em função do tempo. A potência aplicada ao corpo pela empilhadeira é:
Dado: g = 10 m/s²

(FUVEST) Nos manuais de automóveis, a caracterização dos motores é feita em CV (cavalo-vapor). Essa unidade, proposta no tempo das primeiras máquinas a vapor, corresponde à capacidade de um cavalo típico, que consegue erguer, na vertical, com auxílio de uma roldana, um bloco de 75 kg, à velocidade de 1 m/s. Para subir uma ladeira, inclinada como nessa figura, um carro de 1000 kg, mantendo velocidade constante de 15 m/s (54 km/h), desenvolve uma potência útil que é de, aproximadamente, de:

(ITA) Um automóvel de massa m = 500 kg é acelerado uniformemente a partir do repouso até uma velocidade escalar v₁ = 40 m/s em t₁ = 10 segundos, em uma trajetória retilínea. Despreza-se o efeito do ar. A potência média e a potência no instante t₁ desenvolvidas pelas forças do motor de automóvel são, respectivamente:
(Unesp) Uma minicama elástica é constituída por uma superfície elástica presa a um aro lateral por 32 molas idênticas, como mostra a figura. Quando uma pessoa salta sobre esta minicama, transfere para ela uma quantidade de energia que é absorvida pela superfície elástica e pelas molas.

Considere que, ao saltar sobre uma dessas minicamas, uma pessoa transfira para ela uma quantidade de energia igual a 160 J que 45% dessa energia seja distribuída igualmente entre as 32 molas e que cada uma delas se distenda 3,0mm.
Nessa situação, a constante elástica de cada mola, em N/m, vale
(FUVEST) Um automóvel possui um motor de potência máxima P0. O motor transmite sua potência completamente às rodas. Movendo-se em uma estrada retilínea horizontal, na ausência de vento, o automóvel sofre a resistência do ar, que é expressa por uma força cuja magnitude é F = AV², onde A é uma constante positiva e V é o módulo da velocidade do automóvel. O sentido dessa força é oposto ao da velocidade do automóvel. Não há outra força resistindo ao movimento. Nessas condições, a velocidade máxima que o automóvel pode atingir é V0. Se quiséssemos trocar o motor desse automóvel por um outro de potência máxima P, de modo que a velocidade máxima atingida nas mesmas condições fosse V = 2 V0, a relação entre P e P₀ deveria ser:
(ITA) Um navio navegando à velocidade constante de 10,8 Km/h, consumiu 2,16 toneladas de carvão em um dia. Sendo h = 0,10 o rendimento do motor e q = 3,00 x 10⁷ J/kg o poder calorífico de combustão do carvão, a força de resistência oferecida pela água e pelo ar ao movimento do navio tem intensidade igual a:
(UFC) Um homem, arrastando 1 caixa, sobe um plano inclinado de 100m de comprimento e 10 m de altura, com velocidade constante, desenvolvendo no trajeto uma certa potência. Resolvendo trazer a caixa de volta, o homem arrasta a caixa plano abaixo com certa velocidade constante, desenvolvendo a mesma potência que na subida. Se o módulo da força resistiva sobre a caixa é 1/5 do seu peso, podemos afirmar que a velocidade de descida é igual a:
(FUVEST) Deseja-se construir uma usina hidrelétrica aproveitando uma queda d’água de 10m de altura e vazão de 1,0 m³ por segundo. Qual a potência teórica máxima dessa usina?
Dados: densidade da água = 1,0. 10³ kg. m\(^{-3}\)
aceleração da gravidade = 10 m. s\(^{-2}\)
Você chegou ao fim dessa aula com sucesso!
Selecione o botão avançar para seguir para a próxima aula.