Vetores são grandezas físicas que não podem ser definidas apenas por seus módulos, sendo necessários direção e sentido para sua completa compreensão.
Representação de um vetor

É preciso compreender que somente é possível somar vetores de mesma natureza física, não sendo possível, por exemplo, somar um vetor velocidade com um vetor campo elétrico.
É um método utilizado para a soma vetorial no qual os vetores são dispostos de tal forma que a origem de um primeiro vetor deve coincidir com a extremidade do segundo vetor e assim sucessivamente para n vetores. O vetor resultante é dado pela ligação da origem do primeiro vetor à extremidade do vetor n (último vetor).

\[\overrightarrow{\text{A}}\ \text{+}\ \overrightarrow{\text{B}}\ \text{=}\ \overrightarrow{\text{B}}\ \text{+}\ \overrightarrow{\text{A}}\ \text{=}\ \overrightarrow{\text{R}}\]
A regra do paralelogramo é utilizada quando temos dois vetores de mesma natureza e desejamos obter a soma destes vetores, ou seja, o vetor resultante. A regra do paralelogramo é fundamentada na lei dos cossenos, na qual o módulo do vetor resultante é dado pela equação:
\[c^2~=~a^2~+~b^2~+~2~·~a~·~b~·~cos(θ)\]
Onde a, b e c são os módulos dos vetores, e θ é o valor do ângulo entre os vetores somados.
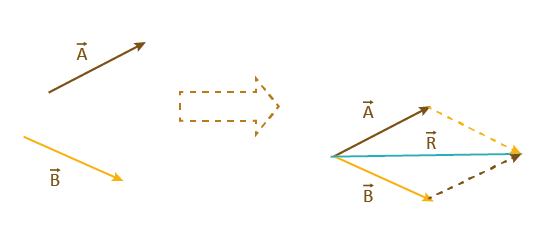
\[\overrightarrow{\text{A}}\ \text{+}\ \overrightarrow{\text{B}}\ \text{=}\ \overrightarrow{\text{R}}\]
Lidando com vetores bidimensionais, em alguns casos é possível simplificar a soma dos vetores separando suas componentes horizontais e verticais, posteriormente somar a resultante horizontal com a resultante vertical, obtendo-se dessa forma a resultante dos vetores somados inicialmente. Os vetores são decompostos da seguinte maneira:

\[\begin{align} &{{\overrightarrow{\text{a}}}_{\text{x}}}\ \text{=}\ \text{a}\ \cdot \ \text{cos}\ \text{( }\!\!\theta\!\!\text{ )} \\ &{{\overrightarrow{\text{a}}}_{\text{y}}}\ \text{=}\ \text{a}\ \cdot \ \text{sen}\ \text{( }\!\!\theta\!\!\text{ )} \\ \end{align}\]
(FGV-SP) São grandezas escalares:
(CEFET-PR) Verifique quais são as grandezas escalares e vetoriais nas afirmações abaixo.
1) O deslocamento de um avião foi de 100 km, na direção Norte do Brasil.
2) A área da residência a ser construída é de 120,00 m².
3) A força necessária para colocar uma caixa de 10 kg em uma prateleira é de 100 N.
4) A velocidade marcada no velocímetro de um automóvel é de 80 km/h.
5) Um jogo de futebol tem um tempo de duração de 90 minutos.
Assinale a alternativa que apresenta a sequência correta.
(UFMG) Uma pessoa sai para dar um passeio pela cidade, fazendo o seguinte percurso: sai de casa e anda 2 quarteirões para o Norte; dobra à esquerda andando mais 2 quarteirões para Oeste, virando, a seguir, novamente à esquerda e andando mais dois quarteirões para o Sul. Sabendo que cada quarteirão mede 100m, o deslocamento da pessoa é:
(UFC-CE) Analisando a disposição dos vetores BA, EA, CB, CD e DE, conforme figura a seguir, assinale a alternativa que contém a relação vetorial correta.

(PUC-RJ) Os ponteiros de hora e minuto de um relógio suíço têm, respectivamente, 1 cm e 2 cm. Supondo que cada ponteiro do relógio é um vetor que sai do centro do relógio e aponta na direção dos números na extremidade do relógio, determine o vetor resultante da soma dos dois vetores correspondentes aos ponteiros de hora e minuto quando o relógio marca 6 horas.
(CFT-CE) Para se posicionar frente ao gol adversário, um jogador efetua deslocamentos rápidos e sucessivos em linha reta com módulos de 1,8 m e 2,4 m, deixando completamente para trás a defesa oponente.
Para que o deslocamento resultante da bola seja de 3,0m, o ângulo entre estes deslocamentos deve ser de:
(CFT-CE) Dados os vetores “a”, “b”, “c”, “d” e “e” a seguir representados, obtenha o módulo do vetor soma:

\[\overrightarrow{\text{R}}\ \text{=}\ \overrightarrow{\text{a}}\ \text{+}\ \overrightarrow{\text{b}}\ \text{+}\ \overrightarrow{\text{c}}\ \text{+}\ \overrightarrow{\text{d}}\ \text{+}\ \overrightarrow{\text{e}}\]
(FATEC-SP) Um automóvel percorre 6,0 km para o norte e, em seguida 8,0 km para o leste. A intensidade do vetor posição, em relação ao ponto de partida é:
(INATEL- MG) João caminha 3 metros para oeste e depois 6 metros para o sul. Em seguida, caminha 11 metros para leste. Em relação ao ponto de partida, podemos afirmar que João está:
(MACKENZIE-SP) Com seis vetores de módulo iguais a 8u, construiu-se o hexágono regular abaixo. O módulo do vetor resultante desses seis vetores é:

(FCC-SP) Qual é a relação entre os vetores \(\overrightarrow{\text{M}}\text{,}\ \overrightarrow{\text{N}}\text{,}\ \overrightarrow{\text{P}}\text{,}\ \text{e}\ \overrightarrow{\text{R}}\) representados abaixo?

(UnB-DF) Sobre a composição dos vetores a seguir podemos dizer que:

(UnB-DF) É dado o diagrama vetorial da figura. Qual a expressão correta?

(UnB-DF) Considere um relógio com mostrador circular de 10 cm de raio e cujo ponteiro dos minutos tem comprimento igual ao raio do mostrador. Considere esse ponteiro como um vetor de origem no centro do relógio e direção variável. O módulo da soma dos três vetores determinados pela posição desse ponteiro quando o relógio marca exatamente 12 horas, 12 horas e 20 minutos e, por fim, 12 horas e 40 minutos é, em cm, igual a:
(UNEB-BA) Um jogador de golfe necessita de quatro tacadas para colocar a bola no buraco. Os quatro deslocamentos estão representados na figura abaixo.

Sendo d₁ = 15 m, d₂ = 6,0 m, d₃ = 3,0 m e d₄ = 1,0 m, a distância inicial da bola ao buraco era, em metros, igual a:
(UFRN) – A figura abaixo representa os deslocamentos de um móvel em várias etapas.
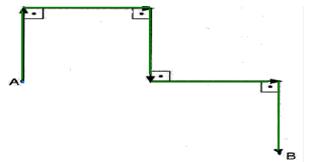
Cada vetor tem módulo igual a 20 m. A distância percorrida pelo móvel e o módulo do vetor deslocamento são, respectivamente:
(FATEC-SP) Duas forças têm intensidades F1=10N e F2=15N. O módulo da resultante da soma vetorial desses dois vetores, não pode ser:
(PUC-RJ) Um veleiro deixa o porto navegando 70 km em direção leste. Em seguida, para atingir seu destino, navega mais 100 km na direção nordeste. Desprezando a curvatura da terra admitindo que todos os deslocamentos são coplanares, determine o deslocamento total do veleiro em relação ao porto de origem.
(Considere √2 = 1,40 e √5 = 2,20)
(UFAL-AL) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à primeira. A distância em linha reta, da caverna ao lago era, em metros:
(AFA) Os vetores \(\overrightarrow{\text{A}}\) e \(\overrightarrow{\text{B}}\), na figura abaixo, representam, respectivamente, a velocidade do vento medida em relação ao solo e a velocidade de um avião em pleno voo, medida em relação ao vento.

Sabendo-se que o movimento resultante do avião acontece em uma direção perpendicular à direção da velocidade do vento, tem-se que o cosseno do ângulo θ entre os vetores velocidades A e B, em módulo, vale:
(MACKENZIE-SP) Um corpo é atirado verticalmente para cima a partir do solo com velocidade inicial de módulo 50 m/s. O módulo de sua velocidade vetorial média entre o instante de lançamento e o instante em que retorna ao solo é:
(PUC-SP) Se a velocidade vetorial de um ponto material é constante e não nula, sua trajetória:
(UFRN) A figura abaixo representa o deslocamento de um móvel em várias etapas. Cada vetor tem módulo igual a 20m.

A distância percorrida pelo móvel e a intensidade do vetor deslocamento são, respectivamente:
(FUVEST-SP) Uma partícula tem movimento circular uniforme. Podemos afirmar que:
(FUVEST-SP) Um automóvel executa uma volta completa em uma pista circular, em dois minutos, mantendo constante a indicação do velocímetro. Em um dos pontos da trajetória, a aceleração vetorial do automóvel te módulo igual a 4m/s². O raio da pista é:
(UFPA) Uma partícula percorre, com movimento uniforme, uma trajetória não retilínea. Em cada instante teremos que:
(UECE-CE) Uma partícula puntiforme tem, em certo instante t, a velocidade, em m/s, dada por v₀ = 1,0 \(\widehat{i}\) – 2,0 \(\widehat{j}\) + 5,0 \(\widehat{k}\). Dois segundos depois, sua velocidade, em m/s, é dada por v = 4,0 \(\widehat{i}\) – 2,0 \(\widehat{j}\) + 1,0 \(\widehat{k}\). No intervalo de tempo considerado, o módulo da aceleração média, em m/s², é:
(UFC) Uma partícula de massa m é lançada a partir do solo, com velocidade v0, numa direção que forma um ângulo ø com a horizontal. Considere que a aceleração da gravidade tem intensidade g e que y é a altura medida a partir do solo. A energia cinética da partícula em função da altura y é dada por:

(UEPA-PA) Ao longo do ano muitos pássaros migram de seus locais de origem para diferentes regiões do planeta. Admita que um pássaro migratório se movimente do sul para o norte com velocidade constante de 20km/h, durante 15 minutos, em uma trajetória retilínea. Na sequência ele muda de direção e percorre 5 km, de tal maneira que sua nova velocidade forma um ângulo de 60° com a velocidade inicial. O módulo do deslocamento resultante do pássaro, a partir do ponto inicial, em quilômetros, é:
(UNIUBE-MG) A figura a seguir representa um pêndulo simples que oscila entre as posições A e B, no campo gravitacional terrestre. Quando o pêndulo se encontra na posição P, a sua aceleração resultante é melhor indicada pelo vetor:

Você chegou ao fim dessa aula com sucesso!
Selecione o botão avançar para seguir para a próxima aula.