(ITA) Um corpo de massa m é colocado no prato A de uma balança de braços desiguais e equilibrado por uma massa p colocada no prato B. Esvaziada a balança, o corpo de massa m é colocado no prato B e equilibrado por uma massa q colocada no prato A. O valor da massa m é:

Na figura a seguir, uma esfera rígida se encontra em equilíbrio, apoiada em uma parede vertical e presa por um fio ideal e inextensível. Sendo P o peso da esfera e 2P a força máxima que o fio suporta antes de arrebentar, o ângulo formado entre a parede e o fio e de:

(FEI) Sabendo-se que o sistema a seguir está em equilíbrio, qual é o valor da massa M quando os dinamômetros indicam 100 N cada um?

(UNIRIO) Na figura a seguir, o corpo suspenso tem o peso 100 N. Os fios são ideais e tem pesos desprezíveis, o sistema está em equilíbrio estático (repouso). A tração na corda AB, em N, e:

Uma barra de peso desprezível está em equilíbrio na posição horizontal, conforme o esquema a seguir. As massas de 90 kg e 1,5 kg se encontram em sua extremidade, sendo que o ponto de apoio está a 40 cm da extremidade direita. Qual o valor da distância “x”, do apoio até a extremidade esquerda, para manter a barra em equilíbrio?

(UFMG) Gabriel está na ponta de um trampolim, que está fixo em duas estacas – I e II –, como representado nesta figura: Seja F1 e F2 forças que as estacas I e II fazem, respectivamente, no trampolim. Com base nessas informações, é CORRETO afirmar que essas forças estão na direção vertical e:

(UFMG) Para pintar uma parede, Miguel está sobre um andaime suspenso por duas cordas. Em certo instante, ele está mais próximo da extremidade direita do andaime, como mostrado nesta figura:

Sejam TE e TD os módulos das tensões nas cordas, respectivamente, da esquerda e da direita e P o módulo da soma do peso do andaime com o peso de Miguel. Analisando-se essas informações, é CORRETO afirmar que:

(UFVJM) Uma viga cilíndrica, homogênea, é construída em duas partes, com dois materiais distintos, de densidades dx = 18 g/cm³ e dy = 2 g/cm³. A viga permanece em equilíbrio, na horizontal, quando suspensa na junção das duas partes, como ilustra a figura abaixo:

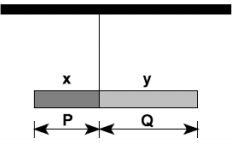
Com base nessas informações, é CORRETO afirmar que a razão adimensional entre as distâncias Q e P (Q/P) é igual a:

(ENEM) Um portão está fixo em um muro por duas dobradiças A e B, conforme mostra a figura, sendo P o peso do portão.

Caso um garoto se dependure no portão pela extremidade livre, e supondo que as reações máximas suportadas pelas dobradiças sejam iguais,

(ITA) Considere o sistema ilustrado na figura abaixo. Supondo-se que tanto a massa da barra AB, como a da polia são desprezíveis, podemos afirmar que

AB está em equilíbrio

(ITA) Uma chapa de aço de duas toneladas está suspensa por cabos flexíveis conforme mostra a figura ao lado, na qual R é uma roldana fixa e P o peso necessário para equilibrar a chapa na posição indicada. Desprezando-se as massas dos cabos, da roldana e o atrito no eixo da mesma, o valor de P deverá ser:

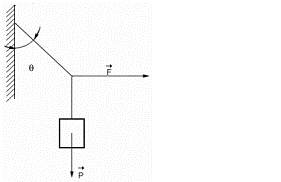
(ITA) Um bloco de peso P é sustentado por fios, como indica a figura. Calcular o módulo da força horizontal F.

(ITA) A barra é uniforme, pesa 50,0 N e tem 10,0 de comprimento. O bloco D pesa 30,0 N e dista 8,0 de A. A distância entre os pontos de apoio da barra é AC = 7,0 m. Calcular a reação na extremidade A.

(ITA) Uma escada rígida de massa 15,0 kg está apoiada numa parede e no chão, lisos, e está impedida de deslizar por um cabo horizontal BC, conforme a figura. Uma pedra de dimensões pequenas e massa 5,00 kg é abandonada de uma altura de 1,80 m acima do ponto A, onde sofre colisão elástica ricocheteando verticalmente. Sabendo-se que a duração do choque é de 0,03s e que a aceleração da gravidade é de 10,0 m.s\(^{-2}\), pode-se afirmar que a tensão no cabo durante a colisão valerá:

(ITA) A figura mostra uma barra de 50 cm de comprimento e massa desprezível, suspensa por uma corda OQ, sustentando um peso de 3000 N no ponto indicado. Sabendo que a barra se apoia sem atrito nas paredes do vão, a razão entre a tensão na corda e a reação na parede no ponto S, no equilíbrio estático, é igual a:

(ITA) É dado um pedaço de cartolina com a forma de um sapinho, cujo centro de gravidade situa-se no seu próprio corpo. A seguir, com o auxílio de massa de modelagem, fixamos uma moeda de 10 centavos em cada uma das patas dianteiras do sapinho. Apoiando-se o nariz do sapinho na extremidade de um lápis ele permanece em equilíbrio. Nestas condições, pode-se afirmar que o sapinho com as moedas permanece em equilíbrio estável porque o centro de gravidade do sistema:

(ITA) Numa balança defeituosa um dos braços é igual a 1,0100 vezes o outro. Um comerciante de ouro em pó realiza 100 pesadas de 1,0000 kg, colocando o pó a pesar um igual número de vezes em cada um dos pratos de balança. O seu ganho ou perda em mercadoria fornecida é:

(ITA) Uma das extremidades de uma corda de peso desprezível está atada a uma massa M₁ que repousa sobre um cilindro fixo, liso, de eixo horizontal. A outra extremidade está atada a uma outra massa M₂, como mostra a figura. Para que haja equilíbrio na situação indicada, deve-se ter:

(ITA) Para que a haste AB homogênea de peso P permaneça em equilíbrio suportada pelo fio BC, a força de atrito em A deve ser:

(ITA) Uma luminária cujo peso é está suspensa por duas cordas AC e BC que (conforme a figura) formam com a horizontal ângulos iguais a P. Determine a força de tensão T em cada corda.

Um pedaço de madeira homogêneo, de seção transversal constante A e comprimento L, repousa sobre uma mesa fixa no chão. A madeira está com 25% de seu comprimento para fora da mesa, como mostra a figura. Aplicando uma força P = 300 N no ponto B a madeira começa a se deslocar de cima da mesa. Qual é o valor real da peso Q da madeira?

(ITA) Considere as três afirmativas abaixo sobre um aspecto de Física do cotidiano.

I - Quando João começou a subir pela escada de pedreiro apoiada numa parede vertical, e já estava no terceiro degrau, Maria grita para ele: - Cuidado João, você vai acabar caindo, pois a escada está muito inclinada e vai acabar deslizando.

II - João responde: - Se ela não deslizou até agora que estou no terceiro degrau, também não deslizará quando eu estiver no último.

III - Quando João chega no meio da escada fica com medo e dá total razão à Maria. Ele desce da escada e diz a Maria: Como você é mais leve do que eu, tem mais chance de chegar ao fim da escada com a mesma inclinação, sem que ela deslize.

Ignorando o atrito da parede:

(ITA) Um brinquedo que as mamães utilizam para enfeitar quartos de crianças é conhecido como mobile. Considere o mobile de luas esquematizado na figura abaixo. As luas estão presas por meio de fios de massas desprezíveis a três barras horizontais, também de massas desprezíveis. O conjunto todo está em equilíbrio e suspenso num único ponto A. Se a massa da lua 4 é de 10g, então a massa em quilograma da lua é:

(EFOMM) A barra indicada na figura, presa de forma articulada ao teto, é composta por dois segmentos. O primeiro segmento \(\overline{\text{AB}}\) possui 4 kg de massa e 10 m de comprimento. Já o segundo (\overline{\text{BC}}\)possui 2 kg de massa e 2 m de comprimento. Sobre a extremidade da barra, atua uma força horizontal para a direita, com intensidade de 35 N.

Se a barra está em repouso, a tangente do ângulo  que ela faz com a vertical vale

(UFRS) A figura mostra uma régua homogênea em equilíbrio estático, sob a ação de várias forças. Quanto vale a intensidade da força F, em N?

(UFPA) Uma barra de secção reta uniforme de 200 kg de massa forma um ângulo de 60° com um suporte vertical. Seu extremo superior está fixado a esse suporte por um cabo horizontal. Uma carga de 600 kg é sustentada por outro cabo pendurado verticalmente da ponta da barra (ver figura). Qual o valor da componente Fx?

(UFSC) É dado o sistema em equilíbrio, e: sen 37° = cos 53° = 0,6 sen 53° = cos 37° = 0,8 Sabendo-se que a tração na corda 1 é 300 N, a tração na corda 2 é:

(ACAFE-SC) Fruto da nogueira (árvore que vive até 400 anos), a noz é originária da Ásia e chegou à Europa por volta do século IV, trazida pelos romanos. Uma característica da noz é a rigidez de sua casca. Para quebrá-la, usa-se um quebra-nozes. A figura abaixo mostra um quebra-nozes, de massa desprezível, facial de ser construído.

Certa noz suporta, sem quebrar, uma força de módulo igual a 2 000 N. É correto afirmar que, para quebrá-la, a distância mínima da articulação, d, em cm, onde se deve aplicar uma força, de módulo igual a 250 N, é:

(UNIOESTE) Uma pessoa usa uma chave de boca para apertar um parafuso, conforme a figura abaixo. A distância do centro do parafuso até a extremidade do cabo da chave de boca é de  e a força  vertical, aplicada a  da extremidade do cabo da chave, possui intensidade

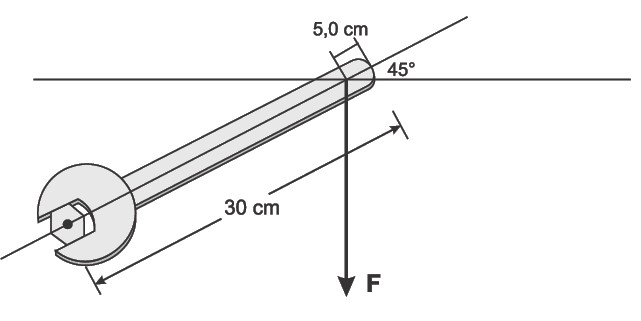
Assinale a alternativa CORRETA.

(UECE) Uma chaminé de 30 m de altura pende, sem se quebrar, até uma inclinação de 30° com a vertical. Considere a aceleração da gravidade como 10 \(\frac{m}{{{s}^{2}}}\)  e o diâmetro da chaminé muito menor que sua altura. Suponha que nessa configuração haja uma força vertical de 1 N puxando rumo ao solo a ponta da chaminé. Nesta situação, o torque exercido por essa força no topo da chaminé vale, em N × m,